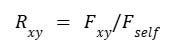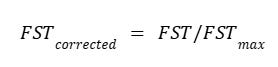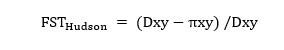Do Parents Ever Share More Genes with Coethnics Than with Hybrid Children?

Insights from the Wright-Harpending Model

Background

A viral claim by neuroscientist and podcaster Jean-François Gariépy (JF Gariepy) asserts that parents are less related to children from interracial unions - in particular between Europeans and Sub-Saharan Africans - than to random European co-ethnics. Gariepy first outlined his argument in a 2020 video (mirrored on altcensored.com). His argument was based on nucleotide differences reported in Yu et al. (2002), which compared genetic variation within and between African, European, and Asian populations. Gariepy has since reiterated and updated this calculation in a recent X post (September 3, 2025), correcting minor numerical errors while maintaining the conclusion. Gariepy acknowledged that similar math for European-Asian and other unions would yield different conclusions, owing to lower inter-population differences.

In response, numerous critics on platforms such as Reddit (e.g., in the r/genetics thread) and X dismissed the claim as nonsense and impossible. For instance, geneticist Razib Khan dismissed the claim, stating in an X reply that, “when you look at all SNPs children are not more distant from you than unrelated of the same race” (September 3, 2025). Critics emphasized that any child inherits exactly 50% of their DNA from each parent, making them far more related than a stranger, regardless of ethnic differences, and criticized the claim for ignoring standard measures of kinship like identity-by-descent. Many stated that the claim represented pseudoscience.

Yet some responses entertained hypothetical scenarios where population divergence could theoretically make parents more related to intra-ethnic strangers than to children. For example, the claim received a sophisticated critique from population geneticist Michael D. Edge (@DocEdge85). DocEdge granted that such a scenario could occur if the genetic distance between populations was large enough. However, DocEdge argued that the required divergence would be much larger than that observed between the populations Gariepy mentioned.

The Wright-Harpending Model

Coefficient of kinship, FST, and coefficient of relationship

A straightforward answer to the question of relative genetic relatedness in multiracial scenarios is not possible, as relatedness can be defined in multiple ways. That said, a standard population genetics approach to this issue can be found in the seminal work of Sewall Wright and in Henry Harpending’s elaboration of it. In this framework, relatedness is understood as the excess gene sharing relative to the metapopulation average (i.e., the overall genetic baseline across all subpopulations under consideration) and to the average within-population variability. A key insight made by Wright (1965; 1969) is that relatedness coefficients can take negative values when individuals are more dissimilar than the metapopulation random expectation, reflecting greater-than-average divergence (Wright, 1965; 1969).

Harpending (2002) elaborates on the equations for the coefficient of kinship (denoted as F) in relation to gene frequencies and to FST, a measure of genetic differentiation between subpopulations. In this model, kinship is conditional on population structure, and the relevant equations, in terms of FST, for an individual are:

The coefficient of relationship (Rxy) between individuals x and y is then derived by normalizing the kinship coefficient relative to self-kinship:

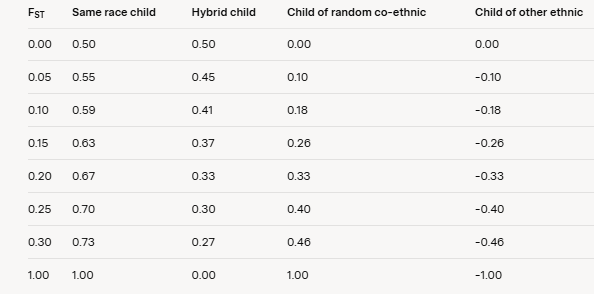
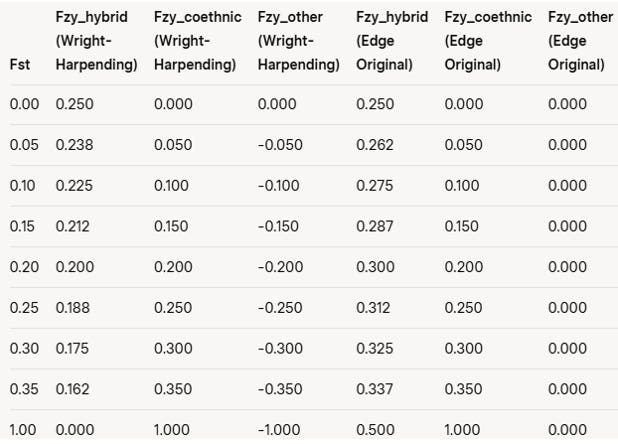
Table 1 presents the coefficients of relatedness based on the Wright-Harpending model. This table illustrates the relationships between same-race children, hybrid children, children of random co-ethnics, and children of other ethnic groups across various pairwise FST values.

Table 1: Coefficients of Relatedness for Different FST Values

Note: The coefficients are derived from the Wright-Harpending framework, where relatedness is measured relative to the metapopulation average, and FST quantifies genetic differentiation between subpopulations.

To determine the point at which a parent’s kinship coefficient with a hybrid child is equal to that with a random co-ethnic stranger, set the coefficient of kinship for the hybrid child equal to FST and solve for FST. According to the Wright-Harpending model, equality is reached at FST = 0.20.

Caveats to the FST Assumptions in the Wright-Harpending Model

The Wright-Harpending model relies on FST to quantify genetic differentiation between subpopulations, with FST ranging from 0 (no genetic differentiation, where all alleles are shared across subpopulations) to 1 (complete differentiation, where no alleles are shared). However, FST is mathematically constrained by within-population genetic variability, particularly heterozygosity and allele frequency distributions. In practice, FST cannot reach 1, even under complete differentiation, as its maximum value is limited by the variability of markers (Alcala & Rosenberg, 2017; Meirmans & Hedrick, 2011).

To address this limitation, various corrections have been proposed. These corrections take the general form of:

where FST_max is the maximum possible FST given the underlying genetic data, taking into account genetic variability.

Shiny APP to explore effects of population structure on relatedness

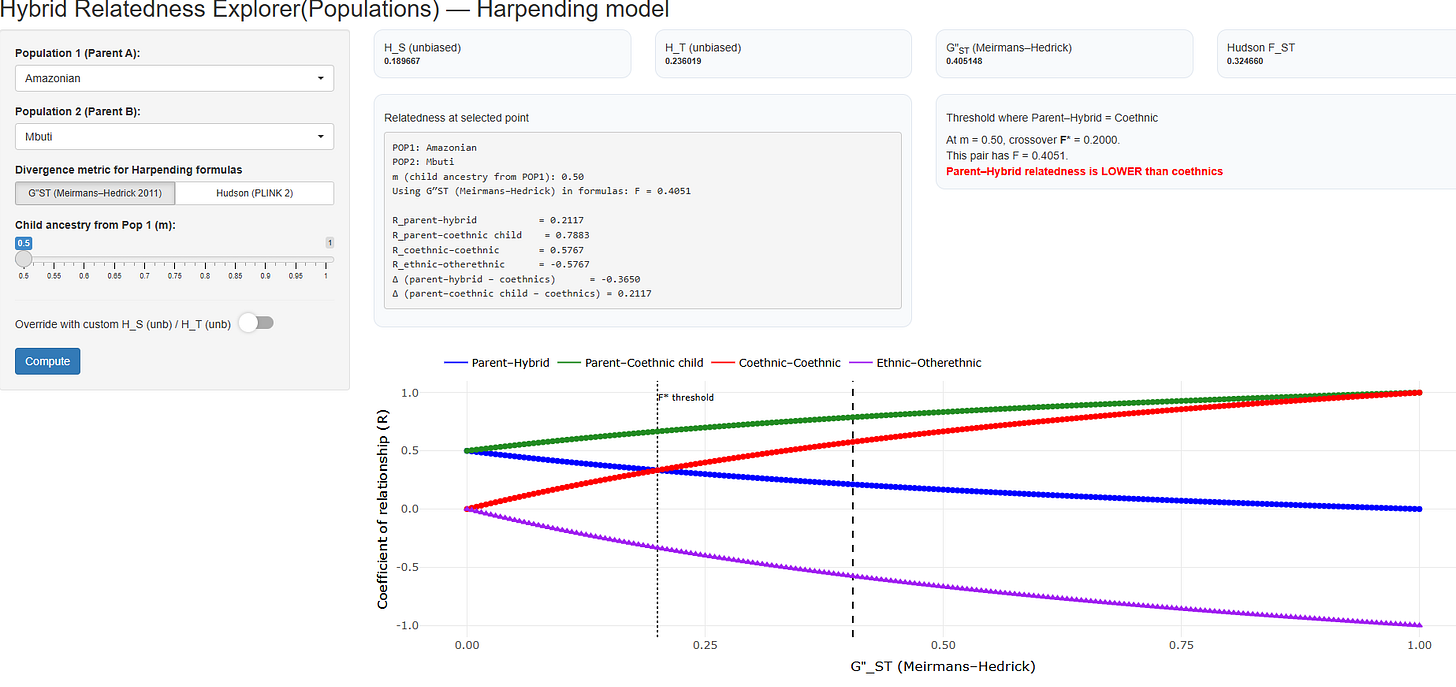
We have created a Shiny app that outputs relationship coefficients for different pairs of populations based on the Wright-Harpending formulas. The app incorporates:

• Hudson's FST Estimator: A robust method accounting for sequence divergence and sample size differences.

• Hedrick's G''ST: A standardized measure based on Nei's (1987) GST, adjusted for heterozygosity constraints. G''ST typically yields larger values than Hudson's FST and can approach 1, making it suitable for computing coefficients of kinship (which assume a mathematical range for FST of 0 to 1).

Example from a pair: in this case, random coethnics are more closely related to the parent than the parent is to the hybrid child.

A Free version of the app can be found here, comprising 14 superpopulations/clusters.

The full version, which covers over 100 populations, is accessible through a link at the bottom of the article and is available only to paid subscribers.

Comparison Between the Wright-Harpending Model, Gariepy’s Approach, and DocEdge’s Model

As noted above, the question of whether a parent is more related to a hybrid child than to a random co-ethnic is ambiguous, as relatedness can be quantified in different ways.

Comparison with Gariepy’s Approach

The Wright-Harpending model employs standard FST estimates, such as Hudson’s FST:

where Dxy is the average nucleotide sequence dissimilarity between populations, and πxy is the average nucleotide diversity within the two populations.

Using the Dxy and πxy values from Yu et al. (2002), the paper referenced by Gariepy, the Hudson FST ≈ 0.161. This aligns with typical FST estimates between Europeans and Sub-Saharan Africans. Applying this FST value to the Wright-Harpending model results in a European parent being somewhat more related to a hybrid child than to a random co-ethnic. Gariepy’s results differ because he uses the sequence dissimilarity (πxy) within only Europeans, rather than the average πxy. Calculating an "asymmetric" FST-like metric based solely on European (or African) population variability yields:

FST-like_European ≈ 0.369 (FST-like_African ≈ -0.048)

Plugging the European-referenced value into the Wright-Harpending formulas produces a result similar to Gariepy’s, suggesting that a European parent is substantially more related to their European coethic than to their hybrid child. Conversely, the African-referenced value implies that an African parent is more related to a hybrid child than to a random African, highlighting an incongruity in this approach (at least given this data (which is based on only 10 Africans and 10 Europeans).

Gariepy’s method measures excess relatedness relative to the genetic diversity within a single population (e.g., Europeans or Africans), whereas the Wright-Harpending model (and the DocEdge model) uses the average. Since within-population genetic diversity (π) varies, with Africans showing greater diversity than other ancestry groups, the results differ. While Gariepy’s approach is valid, it departs from the conventional population genetic framework, where FST is calculated based on average within-population diversity.

Comparison with DocEdge’s Approach

Doc Edge proposed a coalescence model which quantifies genetic relatedness between individuals by measuring the time to their most recent common ancestor relative to the ancestral population’s total coalescence time.

The primary difference between the two models lies in their reference points for relatedness. In the Wright-Harpending framework, kinship is normalized against the metapopulation’s genetic variation, so in a scenario with two completely differentiated clonal lines (FST = 1), each fixed for different alleles, a hybrid offspring has a kinship coefficient of 0 with each parental line, indicating no excess IBD beyond the population baseline. In contrast, Edge’s model, which uses the ancestral population’s coalescence time (t, approximately the inter-deme coalescence time b), assigns a kinship coefficient of 0.5 to the hybrid with each parental line, reflecting direct parental contribution. Consequently, Edge’s model requires a higher FST​ threshold (around FST = 0.33) than does the Wright-Harpending model for a parent to be more related to a coethic than to their hybrid child. These differences in kinship coefficients are summarized in Table 2.

Table 2. Coefficient of kinship in the Wright-Harpending vs. DocEdge Model

The DocEdge approach can be adjusted to normalize relatedness against the metapopulation’s average coalescence time (the expected time for two alleles from the entire population to coalesce), aligning it with the Wright-Harpending framework. When the coalescence model is normalized, the results of the Wright-Harpending framework are recovered.

While relatedness can be defined in multiple ways, the definition used by the Wright-Harpending model aligns more closely with Gariepy’s perspective which concerns relative relatedness between contemporaneous populations. Rooted in Sewall Wright’s population genetics framework (1965), this model measures kinship as the excess probability of identity by descent relative to the metapopulation average.

Summary

The Wright-Harpending model indicates that parents may be more genetically related to random co-ethnics than to their hybrid children, and that the required level of population divergence is not excessive given typical human population differences. Using Hedrick's G''ST values, this scenario applies to populations such as East Asians and Sub-Saharan Africans, who together comprise approximately one-third of the global population.

Furthermore, the model demonstrates that same-race children are significantly more related to their parents than are hybrid children at even modest FST values. For example, at FST = 0.1, the coefficient of relatedness is 0.59 for same-race children compared to 0.41 for hybrid children. The difference is comparable to that between parents and their grandchildren.

Additionally, the model allows us to assess the coefficient of kinship for hybrid relatives (e.g., uncle-nephew or first cousins) by incorporating different coefficients of kinship and FST values. This approach highlights how population divergence affects the kinship with hybrid relatives as compared to co-ethnics and to other relatives.

The app, which covers 100+ populations, and the appendix are available exclusively to paid subscribers.