Why Individual Prediction Doesn’t Scale to Group Differences in Polygenic Scores: Debunking a Common Fallacy
I’m starting to get tired of answering the same objections to polygenic scores (PGS) again and again, so I want to deal with one especially obnoxious criticism here once and for all (hopefully). A recurring misunderstanding in online debates is the claim that a PGS with low individual-level predictive power (say, R² = 0.02) can’t possibly tell us anything meaningful about group differences. From that confusion follow arguments like this:
“Assuming the graph very roughly corresponds to a 0.6 SD increase, and assuming a 0.4 individual-level correlation (which is generous), you’d expect about a 0.24 SD IQ increase (3.6 IQ points).”
This is mathematically correct for individuals, but completely wrong for populations. It conflates two separate statistical questions.
This article explains why the √R² scaling applies only within groups, and why it must not be applied to population differences under polygenic selection.
1. Two Different Questions → Two Different Quantities
(A) Individual-level prediction
Within a population, a PGS with low R² predicts individual outcomes poorly.
If R² = 0.02, then the correlation is:
Thus, if Person A is +1 SD in PGS relative to Person B, we expect only a 0.14 SD difference in their actual phenotype. This gap exists because the PGS captures only a tiny fraction of the factors that determine the outcome. The vast majority of the difference is driven by environmental factors and unmeasured genetics, which ‘dilute’ the predictive power of the score.
(B) Group-level inference
Between populations, we are not trying to predict an individual’s phenotype.
We are trying to detect systematic differences in allele frequencies shaped by selection.
If population A is +1 SD in PGS relative to B, this means:
Alleles associated with the trait increased in frequency in population A.
This difference in PGS reflects real genetic divergence, not random “noise.”
The PGS captures only part of the architecture, but uncaptured causal variants obey the same directional selection pressures.
Thus the +1 SD gap is informative about total genetic divergence, not just about the small slice measured by the SNPs in the PGS.
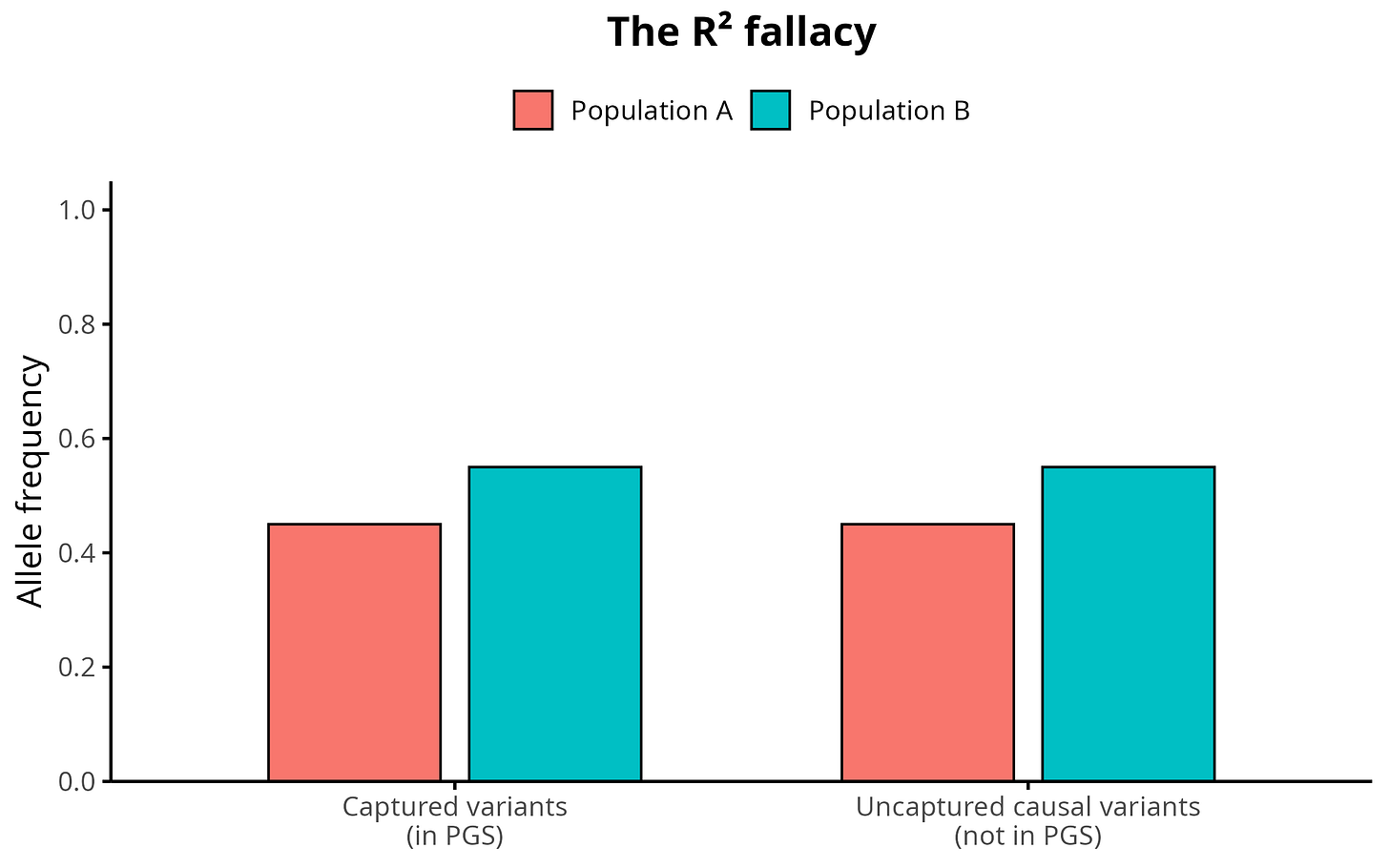
To make this idea concrete, the plot below shows a simple illustration of how polygenic selection affects the underlying architecture. If a trait has been pushed upward by selection, the trait-increasing alleles rise in frequency across the whole genome, not only at the SNPs that happen to be included in the PGS. In other words, the “captured” variants inside the score and the “uncaptured” causal variants outside it both exhibit the same directional allele-frequency shift. The PGS is therefore a sample of this genome-wide pattern, not the full architecture, which is why low individual-level R-squared does not imply that group differences must be mechanically shrunk by √R². The figure shows this visually: the gap between Population A and Population B is identical for both captured and uncaptured variants.
2. The Key Principle: PGS Measures a Sample of the Architecture, Not the Whole Architecture
Polygenic selection acts on the full set of causal variants.
The GWAS-based PGS captures only a subset of these: those discovered and tagged in the GWAS.
But if selection pushed causal alleles in the same direction, then:
The SNPs we observe (PGS SNPs) shift in frequency.
The SNPs we do not observe shift in frequency proportionally.
This is the standard assumption in the polygenic adaptation literature (Piffer 2013; Berg & Coop 2014) and it leads directly to the central error made by critics.
Because selection acts on the underlying effect sizes, trait-increasing alleles are expected to rise in frequency by roughly the same proportional amount at both the variants captured in the PGS and the uncaptured causal variants; the same symmetry applies to trait-decreasing alleles.
3. The Critics’ Fallacy: “Scale the Group Gap by √R²”
Critics implicitly assume:
Only the SNPs inside the PGS diverged between groups.
All the uncaptured causal variants remained identical.
If that were true, then yes, group differences would shrink by √R².
But that assumption is biologically impossible if natural selection acted on the trait.
Selection changes all alleles that contribute to the trait, not just the small fraction discovered in a GWAS.
Thus:
Low R² increases noise, but does not bias the estimate of directional divergence.
The PGS reflects a biased-but-unbiased sample of the architecture.
4. The Height Analogy: Why Partial Measurement Works for Group Differences
Suppose you estimate height using only torso length.
For individuals, this has moderate R². Torso length predicts height well but not perfectly
For groups, if the ratio of torso-to-leg-to-head proportions is roughly constant across groups, then:
A group with longer average torsos is also taller on average.
Measurement error increases noise, not bias.
Applying individual-level R² (torso→height) to group comparisons would imply:
With R² = 0.35, the within-group individual correlation is √0.35 ≈ 0.59:
“Group A has a 5 cm longer torso, so expected height advantage is only
5 × 0.59 ≈ 3 cm, because torso explains 35% of individual height variance.”
This is transparently wrong. Polygenic scores work in a very similar way at the group level.
Example: the Dutch–Spanish (or Croat–Greek) height gap
Northern and Dinaric Europeans are among the tallest in the world. Dutch men average around 183–184 cm, while Southern Europeans such as Spaniards/Greeks are several centimeters shorter on average.
Now imagine we measure only one component of stature such as torso length (sitting height / trunk length), and find:
Dutch mean torso length is +4 cm relative to Spaniards.
At the individual level, torso explains about 35% of height variance.
So, since r= 0.59, a critic applying the individual-prediction logic to group means would conclude: “The Dutch should be only 4 × 0.59 ≈ 2.4 cm taller on average than the Spanish, because torso length explains only 35% of individual height variance.
But this is obviously wrong: it quietly assumes that legs and head size did not diverge at all between populations, even though overall growth processes (genetic and environmental) tend to shift the whole body together. If Dutch and Spanish body proportions are broadly similar, as we expect for closely related European groups, then a +4 cm mean shift in torso length implies a comparable mean shift in total height, not a √R²-shrunk one.
5. Polling as analogy
Polling is a clean analogy for why low individual-level R² doesn’t invalidate group-level inference from PGS. A poll measures a tiny fraction of voters, yet we treat the sample’s mean difference between parties as an estimate of the population’s mean difference, not as something to be “shrunk” by the fraction sampled. We do this because the poll is assumed to be an unbiased slice of the full distribution: sampling fewer people raises uncertainty (wider margins of error) but doesn’t systematically push the estimated gap toward zero. Polygenic scores play the same role. A PGS captures only a subset of the causal variants, so within a population it predicts individuals noisily (low R²), but across populations a mean PGS gap is still an unbiased indicator of directional genetic divergence as long as the measured variants are a representative sample of the architecture and selection shifted the whole set of causal alleles in the same direction.
Multiplying a group PGS gap by √R² is equivalent to saying a poll lead must be multiplied by √(sample fraction), which would only make sense if everyone not sampled were assumed to show zero difference by definition. In both polling and PGS, small samples make the estimate foggier, not smaller.
6. The Correct Interpretation: What a +1 SD PGS Gap Actually Means
If population A is +1 SD above population B in a PGS:
Alleles associated with the trait shifted upward in frequency.
Under proportional selection on the whole architecture, uncaptured alleles also shifted.
Thus the true genetic difference in the latent trait is likely on the same order as the PGS difference, not scaled by √R².
Low R² means the estimate is noisy, not biased downwards.
7. Caveats and Limitations
The argument above explains why low individual-level R-squared does not mechanically shrink group differences, but several important caveats remain.
1. GWAS effect sizes may not transport cleanly across populations.
Polygenic scores assume that the effect sizes estimated in the discovery population apply to other groups. In reality, differences in LD structure, allele frequencies, environmental interactions, imputation quality, and GWAS bias can distort effect estimates when applied cross-population. This means the direction of divergence may be robust, but the magnitude is more fragile.
2. LD decay weakens tagging of causal variants.
If a PGS SNP is only a proxy for the true causal variant, and LD between them differs across populations, the PGS will misrepresent the true allele-frequency shift. This can cause attenuation or exaggeration of population differences depending on how LD patterns differ. This is a limitation of PGS portability, not of the proportional-selection argument itself.
3. The proportional-selection assumption may not hold universally.
The key logic that captured and uncaptured variants shift in parallel depends on the assumption of directional polygenic selection acting roughly proportionally to effect sizes. If a trait has not been under sustained directional selection, or if selection pressures differed across components of the architecture, then the PGS–trait relationship may be more idiosyncratic.
4. Demographic history can mimic or obscure selection.
Population divergence in allele frequencies can result from drift, bottlenecks, founder effects, or mixture, not only selection. When demographic events align with GWAS effect directions by chance, a PGS can show spurious differences. In practice, distinguishing drift from selection requires careful modeling and ideally ancient DNA time series.
5. Residual confounding in GWAS can propagate into group comparisons.
If the original GWAS is affected by stratification or unmodeled environmental structure, these biases could also appear in group differences, even if the logic about R² remains correct.
6. Low R² still matters by increasing noise and uncertainty.
Although low R² doesn’t justify shrinking group differences by √R², it does mean that estimates of divergence will be noisier, more assumption-dependent, and more sensitive to sampling error in effect sizes. Low R² increases uncertainty, not bias.
8. Conclusion: Low R² Doesn’t Shrink Group Gaps, But It Does Affect Confidence
Individual prediction and population divergence are different inferential tasks.
A PGS with relatively low R² is a foggy lens for individuals but still a valid directional detector of polygenic divergence across populations.
Scaling population differences by √R² is mathematically invalid unless one assumes selection acted only on the SNPs in the PGS, an assumption no biologist believes.
References
Berg JJ, Coop G (2014). A Population Genetic Signal of Polygenic Adaptation. PLoS Genet 10(8): e1004412. https://doi.org/10.1371/journal.pgen.1004412
Piffer, D. (2013). Factor Analysis of Population Allele Frequencies as a Simple, Novel Method of Detecting Signals of Recent Polygenic Selection: The Example of Educational Attainment and IQ. Mankind Quarterly, 54(2), 168–200. https://doi.org/10.46469/mq.2013.54.2.3



thank you! this objection can be intuitively crushed by just appealing to law of large numbers, but its great for you to lay it out in mathematically formal terms